連立一次方程式
CGS法のキャッシュヒット率向上法
3次元格子から導かれる連立一次方程式をCGS法で解く際には、 次のような配列変数が使われます。
real(8), dimension(maxi,maxj,maxk,7) :: a
real(8), dimension(maxi,maxj,maxk) :: b, dd, p, q, r, r0, e, h, w
これらのうち、pとwは、MPI並列化で糊しろ交換が必要になるので、 そのままにしておきます。 残りの配列を、次のように1個にまとめます。
real(8), dimension(15,maxi,maxj,maxk) :: aa
ソースファイルの中でこの配列aaを直接使うと、 ソースファイルを読みにくくなるので、 次のようにプリプロセッサーマクロで変数名をすり替えます。
#define a(i,j,k,l) aa(l,i,j,k) #define b(i,j,k) aa(8,i,j,k) #define dd(i,j,k) aa(9,i,j,k) #define r0(i,j,k) aa(10,i,j,k) #define q(i,j,k) aa(11,i,j,k) #define r(i,j,k) aa(12,i,j,k) #define e(i,j,k) aa(13,i,j,k) #define h(i,j,k) aa(14,i,j,k) #define x(i,j,k) aa(15,i,j,k)
このようにデータ構造を変えると、 同時に使われるデータがメモリ上で隣接しやすくなり、 キャッシュのヒット率が上がります。
なお、プリプロセッサーは、大文字と小文字を区別することに、ご注意ください。
行列の前処理
連立一次方程式
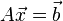
を解くことは、左から正則行列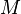 を掛けて
を掛けて
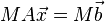
を解くことと同値です。
ここで新しい係数行列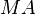 が対角行列に近くなるような
行列
が対角行列に近くなるような
行列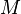 を選べれば、反復法が速く収束します。
このような式の変形を行列の前処理と呼びます。
を選べれば、反復法が速く収束します。
このような式の変形を行列の前処理と呼びます。
もし、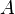 を上三角行列
を上三角行列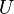 と下三角行列
と下三角行列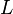 の積に分解できれば、
三角行列の逆行列は後退代入で容易に求まるので、
の積に分解できれば、
三角行列の逆行列は後退代入で容易に求まるので、
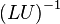 を行列の前処理に使えます。
を行列の前処理に使えます。
完全な行列分解、例えばLU分解やコレスキー分解は、 計算に時間がかかりますし、 疎行列を分解した結果が密行列になってしまいます。 そこで、誤差がある代わりに、疎行列を分解した結果が疎行列になるような 不完全行列分解が前処理に使われています。
行列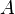 を不完全コレスキー分解してから共役勾配法を使う、
ICCG (Incomplete Cholesky Conjugate Gradient mothod)法が有名です。
を不完全コレスキー分解してから共役勾配法を使う、
ICCG (Incomplete Cholesky Conjugate Gradient mothod)法が有名です。
不完全LU分解法もさかんに研究されています。 並列計算可能な算法があります。 特に、不完全LU分解してから自乗共役勾配法を使う ILUCGS法が、7点差分問題等に使われています(小国力、「行列計算ソフトウェア」)。
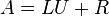
と係数行列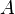 を不完全LU分解します。
を不完全LU分解します。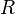 は残差です。
は残差です。
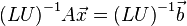
が、もとの問題と等価で、係数行列の質が良くなっています。
しかし、次の問題があります(福井義成他、「新数値計算」)。
不完全行列分解に関して並列計算機への効率のよい実装方法について さまざまな研究が行なわれているが、 未だ決定的なものは提案されていない。
具体的には、三角行列の逆行列とベクトルの積を、 後退代入で計算する部分が、 斜めに処理する算法で並列化可能ではあるものの、 あまり効率よくありません。
前式において、両辺の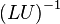 が一致さえしていれば、
不完全LU分解の残差
が一致さえしていれば、
不完全LU分解の残差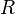 が大きくなっても、
収束に要する反復回数が若干増えるだけで、
連立一次方程式の解に影響はありません。
そこで、並列化しやすいように、不完全LU分解の一部分を0とおく
不完全ブロック分解法があります。
が大きくなっても、
収束に要する反復回数が若干増えるだけで、
連立一次方程式の解に影響はありません。
そこで、並列化しやすいように、不完全LU分解の一部分を0とおく
不完全ブロック分解法があります。
たとえば、行列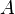 を、次のようなブロック対角行列で近似すると、
近似した行列の逆行列を並列に計算できます。
を、次のようなブロック対角行列で近似すると、
近似した行列の逆行列を並列に計算できます。
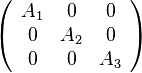
また、上記の小行列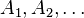 の
逆行列
の
逆行列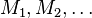 をAMG法で求めて、共役勾配法を加速する、
AMG-CG法があり、AMG法はそのままでは並列化できないという短所を補っています。
をAMG法で求めて、共役勾配法を加速する、
AMG-CG法があり、AMG法はそのままでは並列化できないという短所を補っています。
みずほ情報総研によるAMGソルバによる解析プログラム高速化ライブラリがあります。
筆者コメント:AMG法のフリーソフトがあるか?
ヤコビ法の反復の改良
連立一次方程式を解くヤコビ法では、次の過程が反復されます。
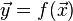
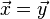
実際のコードで所要時間を測定してみると、 2番目のベクトルのコピーに要する時間がばかにならないことがあります。 そこで、次のような反復過程に改良すると、速くなることがあります。
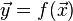
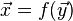
参考文献
一般書籍
- 小国力、村田健郎、三好俊郎、ドンガラJ. J.、長谷川秀彦、
「行列計算ソフトウェア --- WS、スーパーコン、並列計算機 ---」、
丸善、1991年、ISBN4--621--03654--8 アマゾンで調べる - 伊理正夫(いり まさお)、藤野和建(ふじの よりたけ)、
「数値計算の常識」、
共立出版、1985年、ISBN4--320--013343--3 アマゾンで調べる
(文字とおり「常識」として知っておきたい内容が多い。) - 福井義成、野寺隆志、久保田光一、戸川隼人、
「インターネット時代の数学シリーズ2 新 数値計算」、
共立出版、1999年、ISBN4--320--01641--6 アマゾンで調べる - 星守(ほし まもる)、小野令美(おの はるみ)、吉田利信(よしだ としのぶ)、
「新版 入門数値計算 --- チャートによる解説とプログラム ---」、
オーム社、1999年、ISBN4--274--13170--X アマゾンで調べる
(付録の「行列、固有値、2次形式に関する基本的事項」が簡潔で解り易い。) - 戸川隼人(とがわ はやと)、永坂秀子(ながさか ひでこ) 監修、佐藤次男(さとう つぎお)、中村理一郎(なかむら りいちろう) 著、
「よくわかる数値計算 --- アルゴリズムと誤差解析の実際 ---」、
日刊工業新聞社、2001年11月30日、ISBN4--526--04836--4 アマゾンで調べる - 小国力訳、
「行列計算パッケージLAPACK利用の手引き」、
丸善、1995年7月25日、ISBN4--621--04076--6 アマゾンで調べる - 森口繁一 (もりぐち しげいち)
「数値計算術」
共立出版、1987年12月25日、ISBN4-320-02381-1 アマゾンで調べる
(刻み幅の自動調節の話題が特に役立つ。) - 小松勇作、
「数学 英和・和英辞典」、
共立出版、1979年7月15日、ISBN4-320-01282-8 アマゾンで調べる
(数値解析用ソフトウェアの英文マニュアルを読むために便利である。)
マニュアル
- 富士通、「SSL2使用手引書(科学用サブルーチンライブラリ)」、1987年12月、マニュアル番号 99SP--4020--1
論文
- 今村俊幸(いまむら としゆき)、山田進(やまだ すすむ)、町田昌彦(まちだ まさひこ)、
「大規模SMPクラスタにおける固有値ライブラリの通信最適化について」、
情報処理学会HPC研究会報告、2006年 - 小武守恒(こたけもり H.)、長谷川秀彦(はせがわ H.)、西田晃(にしだ A.)、
「OpenMPを用いた並列反復法ライブラリの性能評価」、
第34回数値解析シンポジウム予稿集、pp49-52、2005 http://www.ssisc.org/'