一般逆行列
一般逆行列
数学的背景
一言で説明すると、正方でない行列について、逆行列のようなものを定義しようというのが、 一般逆行列です。
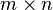 行列Aに対し、
行列Aに対し、
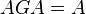
を満足する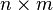 行列
行列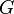 を
を
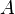 の一般逆行列(generalized inverse)といい
の一般逆行列(generalized inverse)といい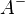 と書きます。
と書きます。
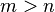 の場合、直線回帰問題
の場合、直線回帰問題
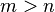 の場合、即ち連立一次方程式
の場合、即ち連立一次方程式
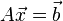
の未知数の数よりも 方程式の数が多い場合には、最小二乗型一般逆行列と、 統計学における最小二乗法による直線回帰が等価です。
直線回帰問題
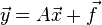
についての正規方程式は
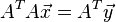
です。
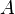 に対し
に対し
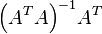
が一般逆行列になります。
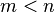 の場合、過小定義問題
の場合、過小定義問題
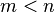 で
で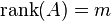 のときは、
のときは、
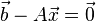 を
正確に満たす無数の解があります。
この場合、
を
正確に満たす無数の解があります。
この場合、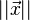 を最小にするただ1つの解
を最小にするただ1つの解
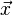 を見つけると、しばしば有用になります。
この問題は過小定義の連立一次方程式に対して
最小ノルム解を見つけることです。
を見つけると、しばしば有用になります。
この問題は過小定義の連立一次方程式に対して
最小ノルム解を見つけることです。
数値例
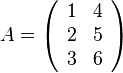
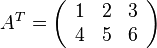
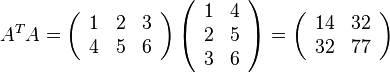
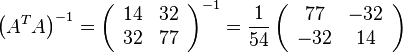
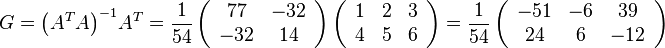
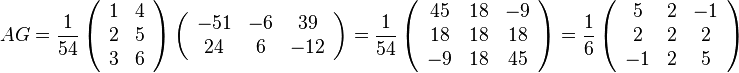
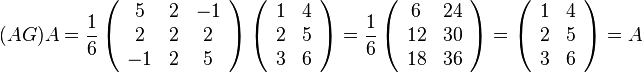
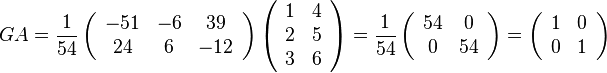
SSL2のGINVの機能
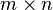 の行列
の行列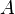 に対して、
次の関係を満足する
に対して、
次の関係を満足する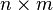 行列
行列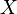 を、
を、
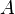 のMoore-Penroseの一般逆行列といいます。
のMoore-Penroseの一般逆行列といいます。
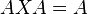
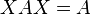
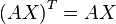

この一般逆行列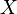 は
は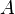 に対して一意的に定まります。
に対して一意的に定まります。
SSL2のGINV (単精度)およびDGINV (倍精度)サブルーチンは、
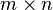 の実行列
の実行列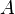 を与えられて、
特異値分解を使い、
を与えられて、
特異値分解を使い、
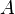 の一般逆行列の転置行列を返します。
の一般逆行列の転置行列を返します。
特異値分解と一般逆行列
一言で説明すると、行列の対角化を、 正方でない行列に一般化したものが、 特異値分解(singular value decomposition)です。
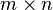 行列
行列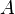 に対して、
に対して、
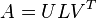
を特異値分解といいます。
ここで、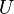 は、
は、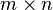 で
で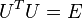 となる行列、
となる行列、
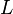 は、
は、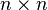 の対角行列、
の対角行列、
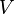 は、
は、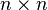 で
で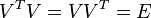 となる行列です。
となる行列です。
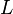 の対角要素
の対角要素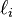 を、
を、
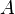 の特異値(singular value)といいます。
の特異値(singular value)といいます。
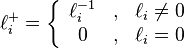
を対角要素とする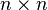 対角行列を
対角行列を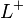 とおきます。
とおきます。
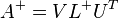
は、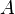 の一般逆行列です。
の一般逆行列です。
特異値分解には、第一にハウスホルダー法で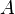 を二重対角行列に変換し、
第二にQR法で対角行列に変換する方法が使われます。
SSLマニュアルのASVD1サブルーチンの項目に、
詳細な解説があります。
を二重対角行列に変換し、
第二にQR法で対角行列に変換する方法が使われます。
SSLマニュアルのASVD1サブルーチンの項目に、
詳細な解説があります。