2次方程式
提供: floatingexception
2次方程式の解法
二次方程式の解法は、純粋数学的には高校二年で解決済みですが、 数値的には深い問題があります。
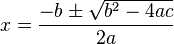
において、加減算で桁落ちが起きて、精度が出ないことがあります。
絶対値が大きいほうの解を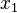 として、もう一つの解を
として、もう一つの解を
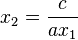
によって求めると、桁落ちが起きません。
数値例を示します。
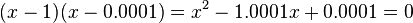
の解は、明らかに1と0.0001ですが、 解の公式をそのまま使うと、次のように大きな誤差が発生します。 Fortranのコードで倍精度演算で求めました。
1.00000000000000000 9.99999999999889865E-0005
改良した方法では、精度が上がります。
1.00000000000000000 1.00000000000000004E-0004
富士通SSL2のDQRDR互換のプログラム例を示します。
! (C) 2007 ISHIKAWA Naota
! This is free software without warranty under new BSD license.
!
subroutine dqrdr2(a0, a1, a2, zz, icon)
implicit none
real(8), intent(in) :: a0, a1, a2
complex(8), intent(out) :: zz(2)
integer, intent(out) :: icon
real(8) :: dd, x1, x2
if (a0 == 0.0d+0 .and. a1 == 0.0d+0) then
icon = 30000
return
else if (a0 == 0.0d+0) then
icon = 10000
zz(1) = -a2 / a1
return
endif
dd = a1 * a1 - 4.0d+0 * a0 * a2
if (dd == 0.0d+0) then
x1 = -a1 / (2.0d+0 * a0)
zz(1) = x1
zz(2) = x1
else if (dd < 0.0d+0) then
x1 = -a1 / (2.0d+0 * a0)
x2 = sqrt(-dd) / (2.0d+0 * a0)
zz(1) = cmplx(x1, x2)
zz(2) = cmplx(x1, -x2)
else
if (0.0d+0 < a1) then
x2 = (-a1 - sqrt(dd)) / (2.0d+0 * a0)
zz(1) = a2 / (a0 * x2)
zz(2) = x2
else
x1 = (-a1 + sqrt(dd)) / (2.0d+0 * a0)
zz(1) = x1
zz(2) = a2 / (a0 * x1)
endif
endif
icon = 0
return
endsubroutine dqrdr2