一般固有値
一般固有値固有ベクトル計算サブルーチンDGSEG2の試作
富士通科学用サブルーチンライブラリSSL2に含まれる、 一般固有値固有ベクトル計算サブルーチン「DGSEG2」と ほぼ互換なサブルーチンを試作しました。
解くべき問題
一般固有値、固有ベクトル問題
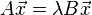 但し、
但し、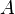 は
は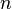 次実対称行列、
次実対称行列、
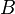 は
は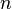 次正値(positive definite、固有値が全て正)対称行列です。
次正値(positive definite、固有値が全て正)対称行列です。
引数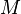 に応じて、固有値を大きい方から、あるいは小さいほうから、
指定された個数だけ求め、それらの固有値に対応する固有ベクトルを求めます。
例えば、
に応じて、固有値を大きい方から、あるいは小さいほうから、
指定された個数だけ求め、それらの固有値に対応する固有ベクトルを求めます。
例えば、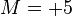 ならば大きいほうから5個の固有値が、
ならば大きいほうから5個の固有値が、
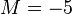 ならば小さいほうから5個の固有値が、計算されます。
ならば小さいほうから5個の固有値が、計算されます。
プログラムインターフェース
SUBROUTINE DGSEG2(A, B, N, M, EPSZ, EPST, E, EV, K, VW, ICON)
INTEGER, INTENT(IN) :: N ! 次数
REAL(8), INTENT(IN) :: A(N(N+1)/2), B(N(N+1)/2) ! 対称行列圧縮モードの行列
INTEGER, INTENT(IN) :: M ! いくつの固有値を求めるか
REAL(8), INTENT(IN) :: EPSZ ! Bのコレスキー分解のピボット0判定値、0.0d+0でデフォルト
REAL(8), INTENT(IN) :: EPST ! 収束判定条件、0.0d+0でデフォルト
REAL(8), INTENT(OUT) :: E(IABS(M)) ! 固有値
INTEGER, INTENT(IN) :: K ! 整合寸法
REAL(8), INTENT(OUT) :: EV(K,IABS(M)) ! 固有ベクトル
REAL(8), INTENT(OUT) :: VW(7*N) ! 作業領域
INTEGER, INTENT(OUT) :: エラーコード、正常ならば0
詳細については、富士通「SSL2使用手引書」 (文書番号99SP-4020-1)の321ページから322ページをご覧ください。
算法
富士通の手引書の表記方法にならい、行列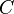 の転置行列を
の転置行列を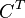 で、
転置行列の逆行列を
で、
転置行列の逆行列を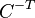 で表わします。
で表わします。
行列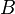 は正値対称行列なので、
は正値対称行列なので、
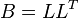
とコレスキー分解できます。
ここで、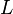 は
は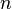 次の下三角行列です。
この計算には、LAPACKの「DPOTRF」サブルーチンを使います。
次の下三角行列です。
この計算には、LAPACKの「DPOTRF」サブルーチンを使います。
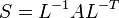
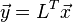
とおくと、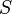 は実対称行列になり、問題の式は
は実対称行列になり、問題の式は
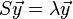
と、標準的な固有値固有ベクトル問題に縮約(reduce)されます。 この計算には、LAPACKの「DSYGST」サブルーチンを使います。
指定された数の固有値を、大きいほうから、あるいは小さいほうから求め、 それに対する固有ベクトルも求めます。 この計算には、LAPACKの「DSYEVX」サブルーチンを使います。 バイセクション法が使われます。
三角行列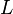 の逆行列を求めます。
これには、LAPACKの「DTRTRI」サブルーチンを使います。
の逆行列を求めます。
これには、LAPACKの「DTRTRI」サブルーチンを使います。
縮約された問題の固有ベクトルを
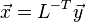
によって、元の一般固有ベクトル問題の固有ベクトルに変換します。 この計算には、BLASの「DTRMV」サブルーチンを使います。
既知の非互換性
SSL2では、固有値の収束判定に使われる絶対誤差の上限が 引数EPSTで与えられますが、 LAPACKでは収束条件がハードコーディングされているらしいので、 この引数は無視されます。
補足
以上の方法でサブルーチンを作成し、互換性を確認したのですが、 版権の都合でソースコードを公表できません。
固有値だけが必要で、固有ベクトルが不要な場合には、もっとうまい方法があります。