Αβ型漸化式
提供: floatingexception
αβ型漸化式
漸化式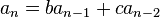 を解くことを考えます。
を解くことを考えます。
もとの漸化式を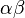 型漸化式に変形します。
型漸化式に変形します。
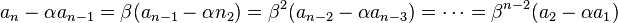
両方の式を比較すると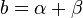 、
、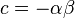 なので、
2次方程式の解と係数の関係より、
なので、
2次方程式の解と係数の関係より、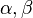 は、
特性方程式
は、
特性方程式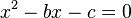 の解となります。
の解となります。
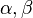 の対称性から、もとの漸化式を次の2つの漸化式に変形できます。
の対称性から、もとの漸化式を次の2つの漸化式に変形できます。
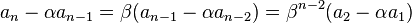
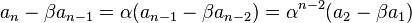
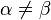 の場合、両辺の差をとります。
の場合、両辺の差をとります。
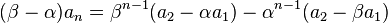
この式を変形して、漸化式を解けます。
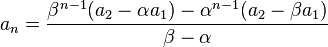
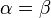 の場合、両辺を
の場合、両辺を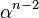 で割ります。
で割ります。
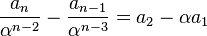
数列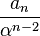 が等差数列になるので、次のように漸化式を解けます。
が等差数列になるので、次のように漸化式を解けます。
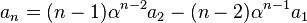
謝辞
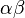 漸化式については、筆者が高校2年の時に、
神奈川県立横浜緑ヶ丘高校の内藤昌孝先生から教わりました。
漸化式については、筆者が高校2年の時に、
神奈川県立横浜緑ヶ丘高校の内藤昌孝先生から教わりました。